算法之枚举（尺取法、前缀和、差分等）

时间复杂度

T(n)表示法

• 时间复杂度是衡量程序的运行速度的量度，它在衡量的时候忽略了硬件的差异
• 它是一个定性描述程序运行时间的数据规模n的关系的函数，这个函数即程序执行基本操作（加减寻址赋值简单的数学函数等）的次数，记做T(n)

for(int i = 1;i <= k;i++){
    ans = (ans + f[n][i]) % mod;
}
// i = 1 执行 1 次
// i <= k 执行 k+1 次（由于i>k的时候还需判定一次，所以还需要在k次的基础上+1）
// i++ 执行 k 次
// 第二行 = + [n][i] % 分别执行 k 次
// T(n) = 1 + (k + 1) + k + 4k = 6k + 2

O(n)表示法

由于T(n)表示法太复杂，所以采取大O表示法

• 大O表示法：考察n趋近于正无穷时的情况
• 当且仅当存在常数 c > 0 和 N >= 1
• 对一切 n > N 均有 |g(n)| <= c|f(n)| 成立
• 称函数g(n)以f(n)为渐进上界或者称g(n)受限于f(n),记做g(n) = O(f(n))

上面写的太过拗口，所以实际计算的时候直接算，忽略低次项和系数即可

以冒泡排序为例：

for(int i = 0; i < len - 1; i++){
    for(int j = 0; j < len - 1 - i; j++){
        if(a[j] > a[j+1])
            swap(a[j], a[j+i]);
    }
}

可以借此得出一个公式，其中C为第二个for循环下if(a[j] > a[j+1]) swap(a[j], a[j+i]);固定的次数

第一层循环中的n当成等差数列相加，并将低次项和系数删除得到
$$
\begin{aligned}
g\left(n\right)&=C\cdot \left(n-1\right)+C\cdot \left(n-2\right)+C\cdot \left(n-3\right)+…+C\cdot 1\\
&=C\cdot \left(\frac{n^2-n}{2}\right)\\
&=O(n^2)
\end{aligned}
$$

举几个例子

1. 看循环

#include <cstdio>
int n,t;
int a[21];

int main( ){
    scanf("%d",&n);
    a[0] = 1;
    a[1] = 3;
    for(int i = 2; i <= n; i++){
        t = 0;
        for(int j = 0;j <= i - 2; j++)
            t = t + a[j];
        a[i] = a[i -1] + 2 * t + 2;
    }
    printf("%d", a[n]);
    return 0;
}

如上所示，循环的次数由输入的n决定，第二个循环的首项为0，末项为 n-2 ，项数为第一个循环的 n-1，所有可以得出
$$
\frac{\left(0+n-2\right)\cdot \left(n-1\right)}{2}=O(n^2)
$$

2. 两个循环

#include <cstdio>
int n,m[21][21];

int main( ){
    scanf("%d",&n);
    for(int i = 1; i <= n; i++){
        for(int j = i; j <= n; j++){
            m[i][j] = i;
        }
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            printf("%3d",m[i][j]);
        }
        printf("\n");
    }
    return 0;
}

第一个循环可表示为$O(n^2)$,第二个相同，所有$O(2n^2)$约掉系数为$O(n^2)$

若碰到 $O(n^3)+O(n^2)$，则将$O(n^2)$约掉

3. 开根号的循环

#include <cstdio>
int n,m;

int main( ){
    scanf("%d",&n);
    for(int i = 2; i * i <= n; i++){
        if(n % i == 0)
            m = n / i;
    }
    printf("%d",m);
    return 0;
}

循环中出现 i * i 的情况，循环只被执行了根号i次，所以时间复杂度为
$$
O\left(\sqrt{n}\right)
$$

4. 固定的循环值

#include <cstdio>
#include <cmath>
int n;
double x,h;

int main( ){
    scanf("%lf",&h);
    for(n = 1; n <= 9; n++){
        x += h;
        h = 0.5 * h;
        x += h;
    }
    printf("%g\n%g",x,h);
    return 0;
}

由于循环的值与输入的值无关，所以运行的时间几乎为固定值，时间复杂度为 O(1)

空间复杂度

Int 32

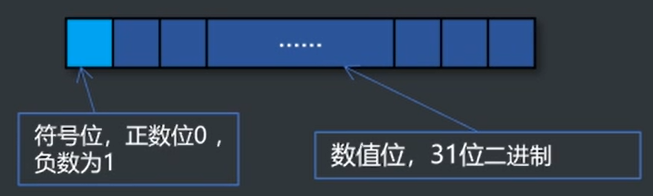
• Long Long : 64位2进制
• Unsigned 用于修饰 int 或者 long long，将符号位变为数值位

Double

double 64位二进制 以科学计数法储存

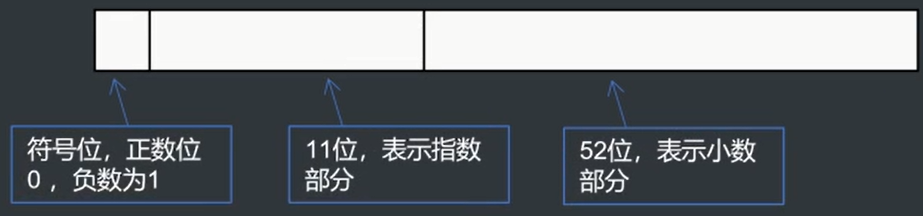
由于小数的特殊储存方式，即使有再多的小数部分，也会丢失些许精度，所以判等可以取|a - b| <= 10^-9 等一定误差范围内的方式

Char

8位二进制（1Byte）

Bool

也是8位二进制

枚举

枚举基本思路

减少枚举次数

1. 选择合适的枚举对象
2. 选择合适的枚举方向 – 方便排除非法和不是最优的情况
3. 选择合适的数据维护方法 – 转化问题

再举几个例子

1. 在一个$N\cdot N \left(N\le 100\right)$矩阵中求一个最大的正方形使得最大的正方形的四个顶点都是有字符 “#” 构成。

   写起来太复杂，考完试再说

2. 给一个数列$\{an\}\left(1\le n\le 100000\right)$，有$q\left(1\le q\le 100000\right)$次询问，每次询问数列的第li个元素到第ri个元素的和。

   1. 用一个数组储存从0到n的每项相加的值，那么 arr[i] = arr[i - 1] + a[i] (a[i]表示数列当前项),所以要查询第 li 个元素到第 ri个元素的和，只需用 arr[ri] - arr[li] 即可
   2. 遍历数列的时间复杂度为O(n)，查询的时间复杂度为O(q)，n和q为次数相同但值可能不同的两个变量，所以总共的时间复杂度为O(n+q)
   3. 其中arr[i]是前缀和

   直接上python伪代码表示一下

   an = [1,3,5,20,21,50,.....] # 设an为已经算出每项值的数组
   arr = [] 
   for i in range(len(an)): 
       sum = arr[i - 1] + an[i] # 这里arr[i - 1]是否为第一项就不判断了
       arr.append(an) # 将计算出来的值插入数组，此循环为O(n)
   # 可假定要查询的数也放在一个二维数组中
   inquiry = [[1,3],[4,10],[100,1000],......]
   for i in inquiry:
       print(arr[i[1]] - arr[i[0] - 1]) # 直接得出答案
       # 此循环为O(q)

3. 给一个数列$\{an\}\left(1\le n\le 100000\right)$，有$q\left(1\le q\le 100000\right)$次修改，每次把数列中的第 a 到第 b 的每个元素都加上一个值 k，求所有的修改之后每个数的值。

   1. 当对第a个到第b个数加上k时，第a个数与第a-1个数的差值增加了k，第b+1个数与第b个数的差值减少了k，而[a,b]区间内部的相邻两个数的差值保持不变
   2. 可新建一个数组arr[i]来保持第i个数与前一个数的差值（第一项可在最前面插入一个0），当需要将[a,b]区间的每个数加上k时，只需要将arr[a]+k，arr[b+1]-k即可
   3. 当所有操作完成时，在将arr[i]去一次前缀和，就可以得到每个元素的值

   an = [1,2,3,4,5,6,7....] # 随机定义一个an数列
   arr = [an[0]] # 因为an第一项与前面相的差值为an[0]本身，所以直接将an[0]加入差值数组
   for i in range(len(an) - 1):
       arr.append(an[i+1]-an[i]) # 计算出数列中所有与前一项相差数
   conditions = [ # 随机定义一组数据 num为需要修改的数，range为修改数组的区间
       {"num": k1,"range": [a1,b1]},
       {"num": k2,"range": [a2,b2]},
       {"num": k3,"range": [a3,b3]},
       {"num": k4,"range": [a4,b4]},
       ......
   ]
   for i in conditions: 
       arr[i["range"][0] - 1] += i["num"] # 区间的第一项+k
       arr[i["range"][1]] -= i["num"] # 区间的最后一项的后一项-k
   result = [arr[0]] # 重新new一个新数组保存结果
   for i in range(len(arr) - 1): 
       result.append(arr[i+1]+result[i]) # 最后将arr[i]都与前一项相加获得结果
   # 时间复杂度为O(n+q)